Resources Center - A discussion on Recurrent Data Analysis using NHPP (Non-Homogeneous Poisson Process) with Power Law

A Poisson Process means the events (failures) inter-arrival times follow exponential distribution, that is, these times are random with constant failure rate.

A Non-Homogeneous Poisson Process with Power Law means the events inter-arrival times follow exponential distribution, but its failure rate u(t) changes with time, according to Power Law (N=λt^β).

u(t)=dN/dt = λβ^t-1

The assumption in this model is that the (repairable) item has infinitely many failure modes (not true in general). Analyst should exercise caution when extrapolating for the results from the model.

Following example illustrates the impact of the above assumption by comparing results using recurring data analysis (NHPP with Power Law) and simulation approach for a system made up of limited renewable components (failure modes).

Followings are the historical failure records for 3 pumps working under similar stress condition. Pump 1 has been operating for a year, while pump 2 and 3 have been operating for 2 years.

Resources_DiscussionRDA1 — Fig.1 Historical failure records for 3 pumps

First, we use recurring data analysis to obtain the NHPP model parameter which allow us to query for future events (failures). Note that the failure modes are ignored in recurring data analysis.

Resources_DiscussionRDA2 — Fig.2 Applying recurring data analysis (Weibull Toolbox, RDA) to the cumulative failure dataset

Resources_DiscussionRDA3 — Fig.3 Cumulative Failures vs Time curve, where λ=1.484 × 10-5 , β=1.891

β greater than 1 implies the pump failure rate increases with time.

The model allows us to extrapolate into the future to estimate failures in the next time interval.

Next, the same system is analyzed using System Reliability approach. We construct the pump system reliability model in terms of its components and generate the failures over 5 years period through simulation.

The pump has 7 failure modes (Figure 1): LSB, ASA, RTR, IPL, SBV, SSL and SWA.

Resources_DiscussionRDA4 — Fig.4 System modeling of pump based on its components

Time-To-Failures for each failure mode are extracted from the historical data.

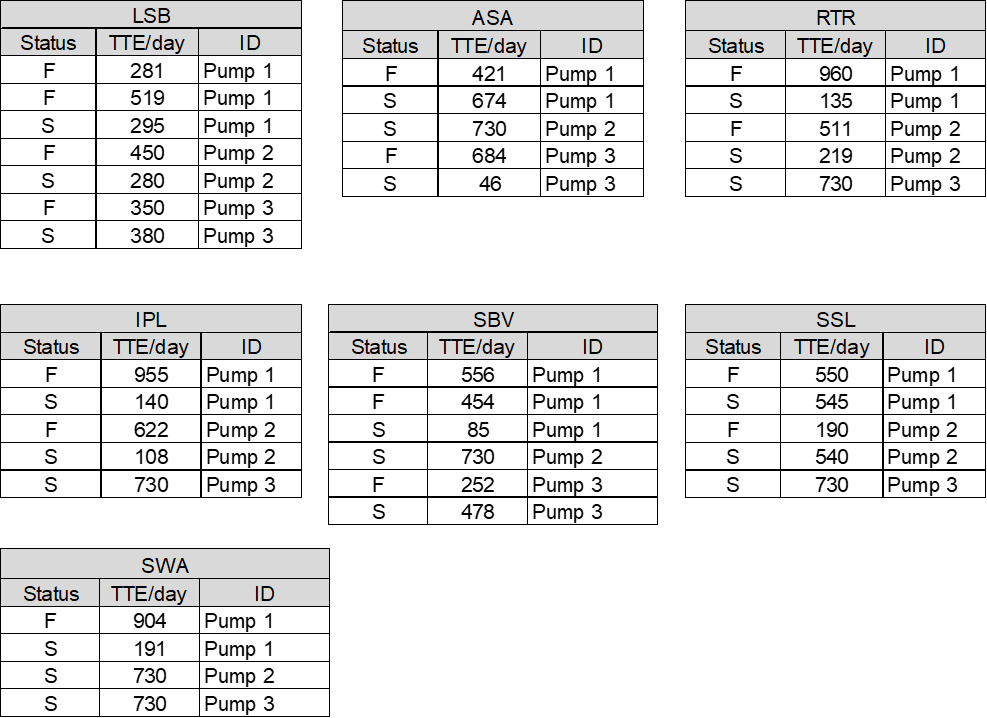
Resources_DiscussionRDA5 — Fig.5 Time-To-Failures for each failure mode

The datasets are fitted to distribution model using LDA module in Weibull Toolbox. Following is the LSB (Line Shaft Bearing) dataset fitted to Weibull distribution, as an example.

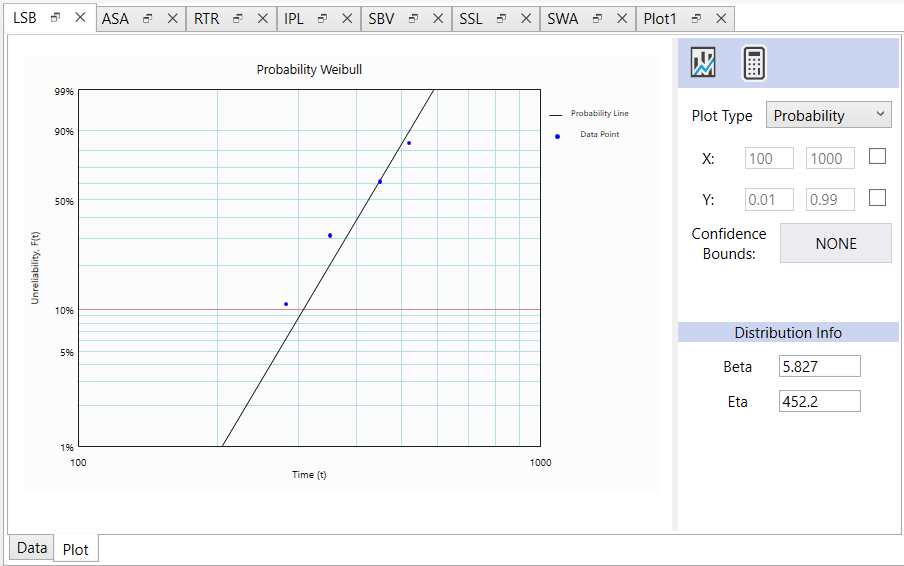
Resources_DiscussionRDA6 — Fig.6 Probability Weibull plot for LSB dataset

The analysis is repeated for the other components. Following is the summary of the pump components’ failure distributions.

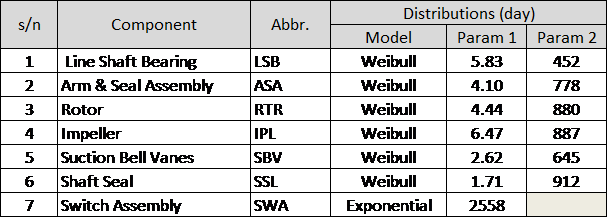
Resources_DiscussionRDA7 — Fig.7 Failure distributions of the pump components

The pump system reliability is modeled in AeROS software.

Resources_DiscussionRDA8 — Fig.8 The pump system reliability

Run a 5-years simulation with 1 execution and the sequence of failures is obtained from the Tri-State plot.

Resources_DiscussionRDA9 — Fig.9 Simulation settings

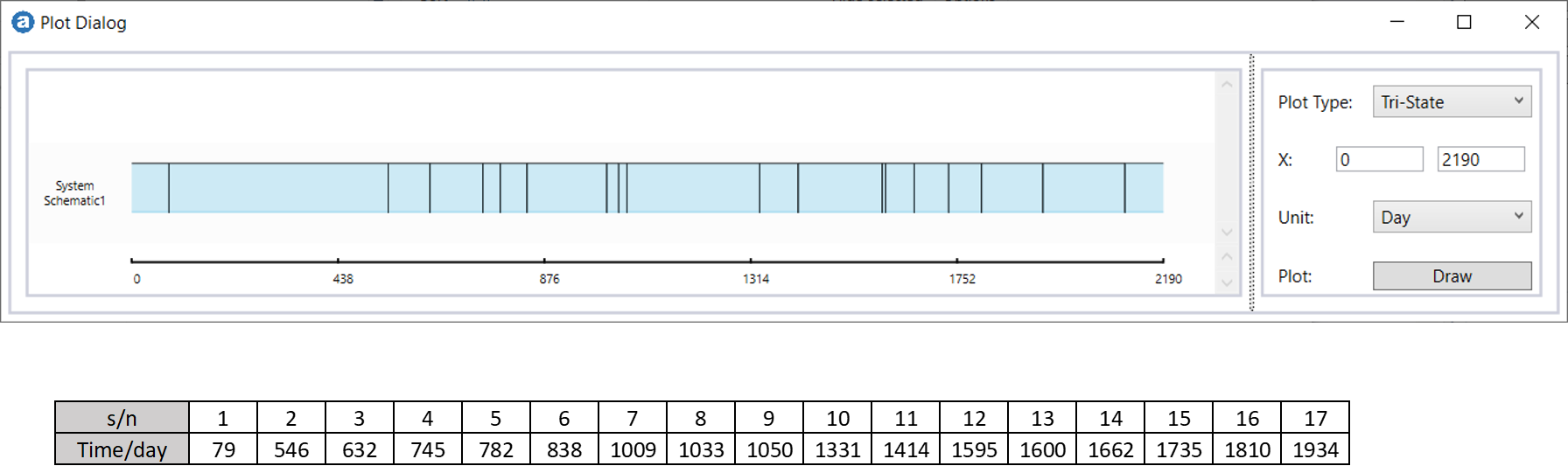
Resources_DiscussionRDA10 — Fig.10 Tri-State plot showing the recurring failures

This cumulative failure times (Green) are superimposed on the Cumulative Failures vs Time plot in Figure 3.

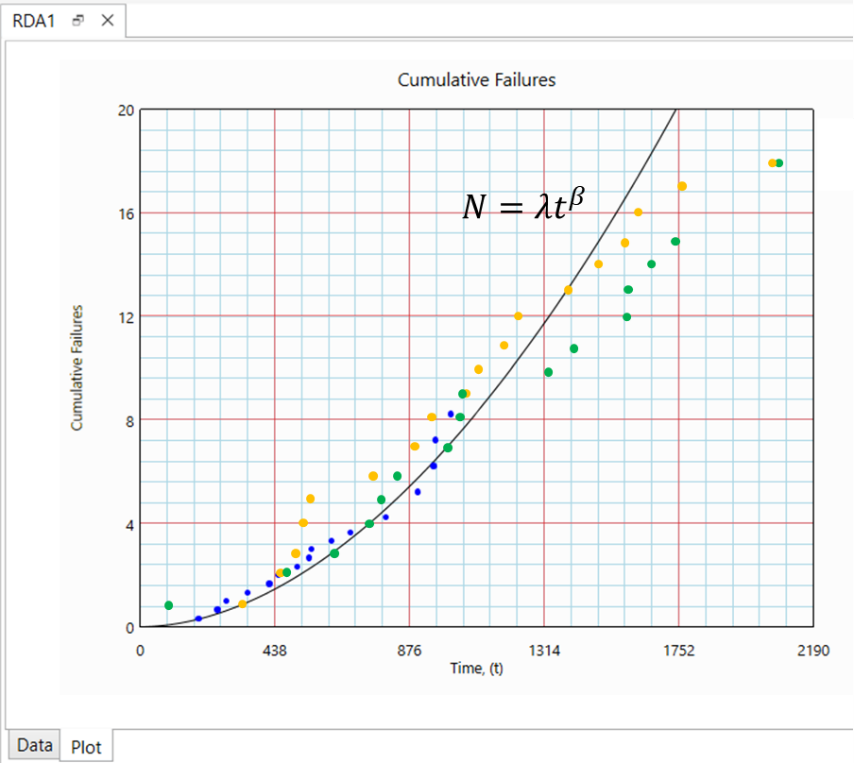
Resources_DiscussionRDA11 — Fig.11 Two sequences of cumulative failure times (Green and Yellow) are superimposed on the Cumulative Failures vs Time plot

Since there are limited number of failure modes, the simulated data will eventually arrive at constant failure rate, while the Power Law (with β>1) curve will continue to band upwards.

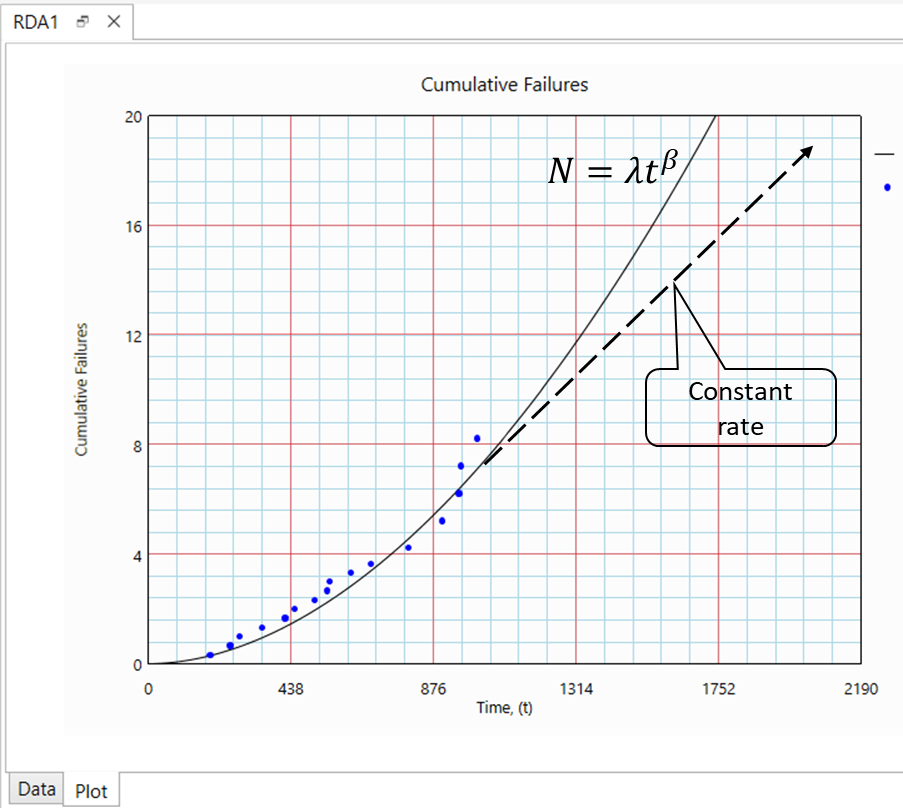
Resources_DiscussionRDA12 — Fig.12 Item with limited number of failure modes deviates from NHPP-with-Power-Law curve

Conclusion

Recurring Data Analysis is significantly easier compared to System Reliability approach. In most practical cases, data are not collected at the lowest actionable item level, as such, only recurring data analysis approach is available for failure projection. Analyst should be aware that this model assumes the (repairable) item has infinitely many failure modes, which is not true in general. Hence analyst has to exercise engineering judgement when extrapolating for the results from the model.

-End-